MACM 101 Discrete Mathematics I
Undergraduate course, Simon Fraser University, School of Computing Science, 2025
A foundational course in mathematics covering basics in discrete mathematics to prepare students for a wide range of courses that require math (e.g., counting, logic, proofs, represetation of numbers).
This is for reference only. For actual outline refer to the course webpage at Canvas (our LMS). Content is subject to change (plus I often update it). This is the schedule I used for Spring 2025.
Course Description
This course is an introduction to discrete mathematics. The course will focus on establishing basic discrete mathematics principles and motivate the relevance of those principles by providing examples of applications in Computing Science.
Course Objectives
This course introduces students to concepts and tools in discrete mathematics, with an emphasis on their applications in Computing Science. By the end of the course, students will be familiar with concepts of discrete mathematics and be able to utilize this in understanding to problems in Computing Science, including recursive thinking, proof of algorithm complexity correctness, and data management.
By the end of this course students should be able to:
- Perform calculations and proofs using discrete mathematics concepts, e.g., counting, induction
- Utilize basic discrete mathematics structures in scenarios where information is managed
- Articulate the relationship between mathematics and computing science
Recommended Textbooks
(The DMA-book) Rosen, K. H. (2019). Discrete mathematics and its applications / Kenneth H. Rosen, Monmouth University, and formerly AT&T Laboratories. (Eighth edition.; International student edition.). McGraw-Hill. SFU Library access
(The DCM-book) Grimaldi, R. P. (2004). Discrete and combinatorial mathematics : an applied introduction / Ralph P. Grimaldi. (5th ed.). Pearson Addison Wesley. SFU Library access
Useful Resources
A list of online resources in case a student is rusty on some of the pre-requisite topics, e.g., doing basic arithmetics by hand, definitions of sequences, notations, distributive laws. These topics are critical (and expected) for each student to be able to keep up with the course.
- Foundational math concepts [LINK]
- Some basic math concepts [LINK]
- Vast collection of math concepts [LINK]
Some of the above are really basic so I recommend students to feel free to skip if they already know.
Here is a more relevant read which can be considered as a supplementary reference [LINK]
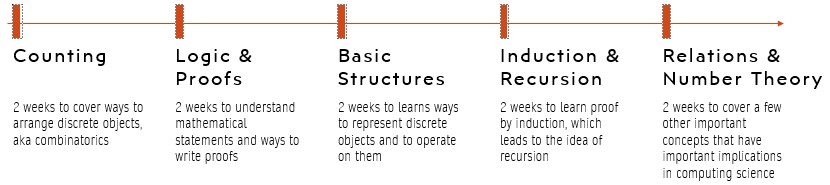
Course Schedule
| Week | Topics | Readings/Watchings1 |
|---|---|---|
| 1 | Course intro
General Math Review | Helpful refresher by College Libraries Ontario [LINK] |
| 2 | Counting (Part 1&2)
| Chapter 6.1-6.5 of the DMA-book Chapters 1 and 5.5 of the DCM-book (1.5 is optional) |
| 3 | Counting (Part 3&4)
| See above |
| 4 | Logic & proofs (Part 1&2)
| Chapters 1.1, 1.2.5, 1.3.1-1.3.4, 1.4.1-1.4.3, 1.4.9, 1.5.1-1.5.3, 1.5.7, 1.6.1-1.6.6, 1.7 of the DMA-book Chapter 2 of the DCM-book |
| 5 | Logic & proofs (Part 3&4)
| See above |
| 6 | Basic structures (Part 1&2)
| Chapter 2 of the DMA-book Chapters 3, 11.1, and 12.1 of the DCM-book |
| 7 & 8 | Reading break & Midterm | - |
| 9 | Basic structures (Part 3&4)
| See above |
| 10 | Induction & recursion (Part 1&2)
| Chapters 5.1-5.4 and 3.2 of the DMA-book |
| 11 | Induction & recursion (Part 3&4)
| See above |
| 12 | Relations (Part 1&2)
| Chapters 9.1, 9.2.1-9.2.3, 9.3 of the DMA-book Chapters 5.1 and 7.1 of the DCM-book |
| 13 | Number theory (Part 1&2)
| Chapters 4.1.1-4.1.4, 4.2.1-4.2.3, 4.3.1-4.3.3, 4.3.6-4.3.8 of the DMA-book Chapter 4 of the DCM-book |
| 14 | Review | - |
| ?? | Final Exam | - |
References in Topics/Readings are for reference only. If there is any topic/concept that is in conflict between class slides and any of these references, what is taught in the classes will be used. ↩
